In questo capitolo si tratta di un particolare tipo di sistemi discreti, cioè dei sistemi "binari". La trattazione è volutamente limitata ai temi essenziali. Per quanto gli argomenti illustrati in questo capitolo non siano sufficienti per poter progettare circuiti digitali, la loro trattazione introduttiva servirà per meglio comprendere il funzionamento dei computer.

Una rete logica è un sistema dinamico nel quale le variabili di ingresso, stato ed uscita sono "binarie", possono cioè assumere solo due valori che indicheremo, in base al contesto, con "1" e "0", oppure con "vero" e "falso" (*), "alto" o "basso" o anche "ON" e "OFF".

Il nome rete "logica" viene proprio dal fatto che ai due valori può essere associato il concetto di vero o falso.

Va da sè che una rete logica è un sistema discreto, dato che non solo ha un insieme discreto di valori, ma quei valori sono solo due.

Le reti logiche più comuni sono le funzioni logiche combinatorie.

Come già visto nel primo capitolo l'uscita di un sistema combinatorio in ogni istante dipende solo dagli ingressi in quello stesso istante.

Tutte le funzioni logiche combinatorie si possono specificare con una tabella che indica quali sono le uscite della funzione in corrispondenza a tutte le possibili combinazioni dei suoi ingressi.

Questa tabella viene detta "tabella di verità" della funzione.

Figura 25: tabella verità di una funzione logica combinatoria con due ingressi e tre uscite (*)

Le uscite indicate in tabella non sono in alcun modo significative

La tabella di verità di una funzione logica è la funzione di uscita del sistema, cioè l'unica funzione del sistema nel caso di nel caso di sistemi combinatori (senza stato):

_ _ _

u(t) = g (i(t))

Le più semplici fra le funzioni logiche sono le funzioni elementari, fra le quali analizzeremo NOT, AND, OR e XOR.

Le reti logiche più complesse, sia combinatorie che sequenziali, si possono ottenere collegando opportunamente i dispositivi con i quali si realizzano le funzioni logiche elementari.

Per specificare come devono essere fatti i collegamenti nelle reti logiche si usano diagrammi, nei quali ciascuna funzione elementare ha il suo simbolo, indicato nel seguito.

La funzione NOT ha un solo ingresso e non fa altro che invertirne il valore.

La sua tabella di verità è dunque la seguente:

Figura 26: tabella di verità di NOT

La presenza di un pallino in un diagramma logico significa che il valore logico presente nel filo ove esso è disegnato viene invertito ("negato").

La funzione AND ha almeno due ingressi ed una sola uscita. L'uscita vale 1 solo quando tutti gli ingressi sono a 1, altrimenti vale 0.

Figura 27: tabella di verità di AND a due ingressi

Come indicato dal suo nome AND è vera solo se l'ingresso 0 e l'ingresso 1 sono veri contemporaneamente.

L'AND viene anche detto "prodotto logico" ed indicato con il simbolo "*".

Si possono avere anche AND a molti ingressi, la cui tabella di verità è corrispondente alla descrizione a parole:

Figura 28: tabella di verità di AND a più di due ingressi

I due punti nella tabella indicano che manca qualcosa, che non è difficile ricostruire ..

La funzione OR è "duale" della AND, ha un'unica uscita che è falsa solo quando tutti i suoi ingressi sono falsi. Perciò OR è vera se uno qualsiasi degli ingressi è vero e si può tradurre in Italiano con "oppure".

Figura 29: tabella di verità di AND

Anche la funzione OR può avere molti ingressi, in modo analogo alla AND. OR viene anche detto "somma logica" ed indicato con il simbolo +.

Il nome XOR sta per exclusive OR ed indica che la funzione è simile ad un OR, salvo che "esclude" il caso in cui tutti gli ingressi sono veri. In tal caso infatti l'uscita è falsa (vedi l'ultima riga della tabella di verità).

Figura 30: tabella di verità di AND

Lo XOR funziona come il segno delle moltiplicazioni algebriche (considerando lo zero il più e l'uno il meno: "più per meno dà meno ..").

Si chiama "porta logica" il dispositivo fisico che realizza una funzione logica elementare.

Data la tabella di verità di una funzione logica combinatoria essa può essere realizzata utilizzando le funzioni logiche elementari. Tecniche matematiche, che non sono tra gli scopi di questo libro, permettono di minimizzare il numero delle porte logiche utilizzate per realizzare fisicamente (sintetizzare) una funzione logica.

Il modo più comune per realizzare una porta logica è l'utilizzazione delle tecnologie elettroniche del transistor, ma, se la funzione è semplice, si possono usare tecnologie elettromeccaniche (relais) o pneumatiche (circuiti in logica pneumatica).

Dato che i relais ed i circuiti logici pneumatici sono ingombranti, essi non si possono utilizzare per realizzare sistemi complessi. Al contrario le porte logiche elettroniche possono essere realizzate in decine di milioni per centimetro quadro. Questa è la ragione per la quale i computer sono realizzati con circuiti elettronici.

In alcuni casi nella tabella della funzione da realizzare fisicamente possono esistere delle condizioni d'indifferenza, nelle quali non importa quale sia il valore del rispettivo ingresso od uscita.

Le condizioni d'indifferenza, "don't care" in Inglese ("non interessa"), si indicano nelle tabelle con un segno "-".

Maggiore è il numero delle condizioni d'indifferenza di una tabella e minore è la quantità di porte richieste dalla realizzazione fisica della funzione. Ne consegue che progettare tabelle con molte condizioni d'indifferenza fa risparmiare sul costo della rete logica realizzata.

Figura 31: una tabella di verità con condizioni d'indifferenza

La riga 4 della tabella significa che se i₁ = 0 e i₀ = 1, indipendentemente da quanto valgano i₂ e i_3, l'uscita u_o deve essere = 0, mentre u₁ può assumere qualsiasi valore, perché, evidentemente, non interessa ai fini pratici.

Analoghi i casi delle altre righe della tabella con le indifferenze. C'è da notare che la tabella ha solo 9 righe, invece delle 16 che servirebbero per coprire tutte le combinazioni degli ingressi senza condizioni d'indifferenza sugli ingressi.

DA FARE

DA FARE

DA FARE

Stati "infiniti" e stati finiti.

DA FARE

In questo paragrafo si propone un esempio di progettazione di un automa.

La prima cosa da dire è che non esistono tecniche obbligatorie o "standard" per inventare un automa, ognuno è libero di fare come gli viene più naturale e con le tecniche che ha affinato personalmente con la pratica.

Quanto illustrato in questa sede corrisponde perciò al modo di realizzare gli automi sviluppato dall'autore, ma può fornire ai lettori spunti per l'elaborazione personale.

Diamo la descrizione a parole dell'automa da realizzare.

Si vuole realizzare la pulsantiera di prenotazione per le domande di un telequiz.

Al gioco partecipano tre concorrenti, che debbono rispondere a domande nozionistiche lette dal presentatore (che chiameremo "Mike").

Quando un concorrente pensa di sapere la risposta pigia, per prenotare la risposta, un tastone a fungo situato nella sua cabina.

L'automa che dobbiamo progettare deve far accendere una luce nella cabina del concorrente che ha spinto per primo il suo tastone.

Gli ingressi del sistema sono: 3 tasti a fungo, uno per ogni concorrente, un tasto per Mike, chiamato "Reset", che gli serve per spegnere tutto e ricominciare daccapo.

Le uscite sono le tre lampadine nelle cabine dei concorrenti. Dovrà rimanere accesa la lampadina del concorrente che si è prenotato per primo, fino a che non viene premuto il tasto "Reset".

Prima di cominciare la spiegazione si consiglia al lettore di spendere un'ora o due per provare da solo a progettare questo automa e quello descritto al Problema B, poi prendere una pausa, infine studiare dalla prossima riga in avanti.

Per prima cosa bisogna immaginare di porre il sistema in una condizione ben determinata, dalla quale cominceremo a disegnare il grafo.

Di solito viene naturale considerare per questo scopo la condizione di "riposo" del sistema, quella in cui è il sistema prima di "cominciare a lavorare". Questo non è obbligatorio. Lo stato da cui si inizia a disegnare un grafo è semplicemente quello che viene più comodo e naturale al progettista.

Nel nostro esempio ci poniamo nella condizione in cui tutto deve ancora cominciare ed il sistema è pronto per accettare le prenotazioni dei concorrenti. Cominciamo a disegnare il primo stato, che chiamiamo "Attesa".

Decidiamo la notazione da usare per gli ingressi e per le uscite. Sia gli ingressi che le uscite sono grandezze binarie "spento" o "acceso". Scriveremo gli ingressi in questo ordine: <B1><B2><B3><Rst>, ovverosia bottone del concorrente 1, poi 2, 3 e, infine, Bottone Reset.

Scriveremo il valore binario dell'ingresso corrispondente, indicheremo la condizione di indifferenza con un -. L'ordine con cui indicheremo le uscite sarà: <L1><L2><L3>, cioè lampada 1, poi 2 e 3. Sulle uscite non potremo imporre condizioni di indifferenza.

Per gli ingressi, se scriveremo 100- vorrà dire: ingresso 1 ON, 2 e 3 OFF, Rst non interessa, può assumere qualunque valore. Le condizioni di indifferenza vengono dette "don't care" ("non importa").

Disegneremo un automa di Moore, perché in questo caso non c'è vantaggio ad usarne uno di Mealy (questo di solito si scopre a posteriori, le prime volte è comunque meglio farli tutti e due per imparare a capire di persona le differenze ed i vantaggi che i due tipi di automi comportano e per fare un po’ di pratica).

Per le uscite, scritte dentro i cerchi degli stati perché l'automa è di Moore, se scriveremo 001 intenderemo: lampade L1 e L2 spente, L3 accesa.

Deciso quale dev'essere il primo stato bisogna vedere cosa cambia in conseguenza dell'arrivo di ogni ingresso. Se arrivano certi ingressi bisognerà immaginare di passare ad altri stati, spesso nuovi. Quando sarà necessario "inventare" nuovi stati? Quando la situazione del sistema cambia, per esempio bisogna "ricordare" qualcosa o si deve effettuare un conteggio. Ciascun nuovo stato deve essere ben caratterizzato e deve avere qualcosa che lo distingue rispetto a tutti gli altri. Quest'ultimo avvertimento è importante per non progettare grafi che abbiamo degli stati in più, ma si tenga comunque presente che esistono delle tecniche automatiche per scoprire se alcuni stati del grafo sono "doppi" e perciò inutili. Utilizzando queste tecniche potremo essere certi di aver realizzato un automa in cui il numero di stati è minimo.

(nota: le tecniche per la minimizzazione degli automi sono al di fuori del campo di interesse di questo libro).

Proseguiamo con il nostro esempio. I nostri concorrenti sono pronti e fino a che nessuno spinge un tasto non deve cambiare niente. Anche se Mike spinge Reset non deve accadere niente, dato che questo è lo stato di "pronti". Ci sarà perciò un autoanello nei casi di ingressi 000-, naturalmente le uscite saranno tutte spente (000). Si può già notare che da ogni punto del grafo, il pulsante di Reset deve far tornare a questo stato (vedi Figura 32).

Figura 32: stato iniziale

Se ora viene premuto uno dei bottoni dei concorrenti, la sua lampada dovrà accedersi. Poi bisognerà fare in modo che rimanga accesa per un tempo sufficiente per farla vedere (Figura 33).

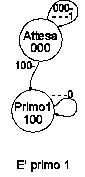Figura 33: è primo 1

Per rimanere per molto tempo in questa condizione di "acceso" è necessario inventare un nuovo stato per ciascuno dei tre bottoni. Li chiameremo Primo1, Primo2, Primo3, per indicare chi è arrivato primo. Naturalmente si passerà a Primo1 solo quando è schiacciato il bottone 1 e gli altri stanno ancora dormendo, cioè gli ingressi sono 1000. Analogamente 0100 farà passare a Primo2 e 0010 farà passare a Primo3, - - - 1 farà tornare ad Attesa (pressione Reset).

Seguiamo ora il ramo di Primo1, dato che anche gli altri rami del grafo saranno analoghi, ma relativi agli altri concorrenti. Per tutto il tempo che l'automa passa in Primo1 si dovrà mantenere accesa la lampada 1 (100). Ora abbiamo trovato il primo, che è l'unico che ci interessa e quindi rimaniamo in questo stato indipendentemente da tutti gli ingressi, tranne Reset che deve essere zero: ciò significa autoanello per - - - 0. Quando arriva Reset si torna allo stato di Attesa (- - - 1), dove si spengono le lampadine (000).

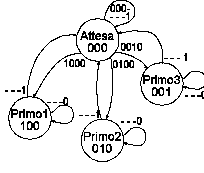Figura 34: grafo completo, rilevazione del primo

Si fa notare che questo automa NON prevede casi in cui più ingressi cambiano contemporaneamente.

Si considera che questo sia un automa asincrono e quindi l'evenienza che due concorrenti spingano i tasti esattamente nello stesso nanosecondo è molto improbabile.

Inoltre se ciò dovesse proprio accadere i circuiti elettronici con cui sarà realizzato l'automa "sceglierebbero" comunque uno dei due stati, perché tale è la loro natura fisica. Perciò si percorrerebbe comunque solo uno dei rami del grafo che abbiamo disegnato, assegnando la vittoria ad uno solo dei tre.

Al contrario se l'automa fosse stato sincrono avremmo dovuto prevedere degli stati e dei percorsi che tenessero conto anche di variazioni contemporanee di uno o più ingressi.

• Problema B

Ora complichiamo il problema e vediamo come deve cambiare la nostra macchina se si vuole permettere la prenotazione anche del secondo concorrente che aveva pigiato il tastone, per fargli la domanda quando il primo sbaglia la risposta.

Per prima cosa bisogna pensare all'operatività dell'automa. Come lo facciamo funzionare, come farà Mike a vedere chi è arrivato secondo? Mike ha già un bottone gli facciamo usare quello (così non si sbaglia!). Quando pigia il bottone una prima volta funzionerà come il "Reset" visto prima; quando lo pigia la seconda volta sarà un "Fa vedere il secondo arrivato".

La parte iniziale del nuovo grafo sarà uguale. Fino a che non si individua il primo tutto procede come nel caso più semplice. A partire dallo stato Primo1 cambia qualcosa. Seguiremo solo il ramo di Primo1, perché gli altri sono analoghi. Primo1 identifica l'arrivo del primo, ma non si sa ancora chi è il secondo. Nell'attesa che uno degli altri pigi il suo tastone rimarremo in questo stato, accendendo la lampada del primo. Non ci interessa più cosa succede nel tasto 1 perché il concorrente l'ha già premuto, noi ce ne siamo accorti, e adesso lo può anche rilasciare o tenere premuto. Per questo l'autoanello su Primo1 ha una condizione d'indifferenza sul tasto 1, gli altri tasti però non sono ancora stati pigiati: ciò significa autoanello con - 000. Non appena arriva il secondo, ce lo dobbiamo ricordare in uno stato. Ne dobbiamo fare due, che chiamiamo Pr1Sec2 (Primo1 e Secondo 2) e Pr1Sec3 (Primo1 e Secondo 3), per ricordarci quale dei due è il secondo. Da notare, è importante, che Pr1Sec2 e Pr1Sec3 mantengono accesa la lampadina del primo, perché quella del secondo si deve vedere solo quando Mike preme il suo tasto, non quando il concorrente lo preme! Infatti l'autoanello su Pr1Sec2 e Pr1Sec3 c'è quando Reset non è premuto. Da notare che da qui in poi non ci si interessa più dei tasti dei concorrenti, perché il primo ed il secondo li abbiamo già rilevati.

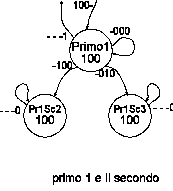Figura 35: primo 1 e il secondo

Seguiamo ora il solo ramo di Pr1Sec2 (vedi

Figura 36

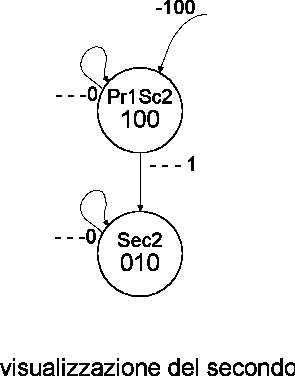
Figura 36: visualizzazione del secondo

Completando il grafo con i rami di tutti gli altri casi si ottiene quello mostrato nella seguente figura:

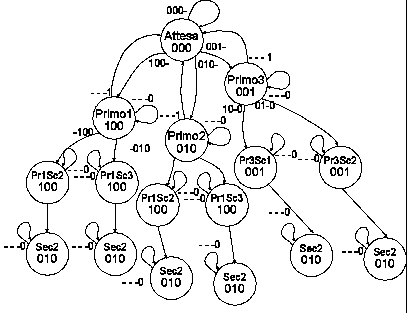
Figura 37: grafo non ottimale

Si noti che Sec2 ha solo il significato "visualizzo il secondo, che è due, aspettando il Reset". Quindi in questo stato non ci importa più di chi fosse stato il primo e possono arrivare qui transizioni che provengono anche dagli altri rami, ove il primo non era il concorrente 1.

Quest'ultima caratteristica dell'automa si può vedere nella figura "grafo completo, primo e secondo". Per accorgersi che potevamo andare da Pr3Sec2 a Sec2 ci voleva un po' di accortezza e di esperienza. Se non ci fossimo accorti che questo si poteva fare, avremmo inserito alcuni stati in più, in modo da averne uno ad ogni fine di "ramo", per visualizzare il secondo arrivato (vedi Figura 37). Come già detto, ci può confortare il pensiero che avremmo potuto scovare ed eliminare questi stati in più con un procedimento meccanico relativamente semplice, da eseguirsi sulla carta o con un programma su computer.

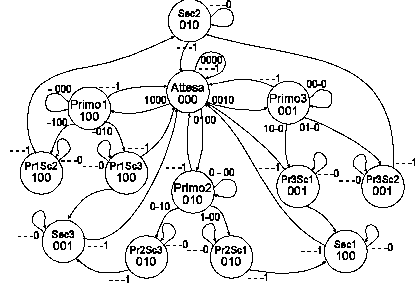Figura 38: grafo completo con rilevazione del primo e del secondo

• Realizzazione di automi con un programma per computer

La realizzazione di automi con dispositivi elettronici non è fra gli scopi di questo libro. Qui si vogliono solo dare consigli per la realizzazione con programmi software di un automa, con un normale linguaggio di programmazione di alto livello.

Il grafo dell'automa è un esempio di buona documentazione di un progetto. Specie se i nomi degli stati e delle transizioni sono assegnati con discernimento esso riunisce in sé molte informazioni, è di comprensione non complicata (una volta che ci si è abituati al suo "linguaggio") e può essere di grande aiuto anche nella fase di stesura del codice. Per questo non è da scartare l'ipotesi di disegnare automi anche per la documentazione di programmi normali. L'automa, se non è troppo complicato e non se ne perde il "controllo", è infatti una rappresentazione estremamente significativa del funzionamento di un programma.

La realizzazione in software di un automa è molto semplice.

Si definisce una variabile, p.es.:

DIM StatoDellAutoma as Integer (*)

(*) Non è scopo di questo testo trattare il linguaggio Visual BASIC, per cui il lettore dovrà trovare altrove i dettagli sulla sintassi delle istruzioni del linguaggio. Le istruzioni BASIC utilizzate sono comunque molto semplici ed il listato dovrebbe essere comprensibile comunque.

Questa variabile assumerà un valore diverso per ciascuno degli stati presenti nel grafo.

Il programma dovrà partire con l'automa posizionato in uno stato specifico, tipicamente lo stato di "riposo" del sistema; p.es.

<CODICE>

StatoDellAutoma = 1

</CODICE>

Da questo punto il programma non è che un ciclo continuo contenente una istruzione di selezione che ha un CASE per ogni stato e che tratta ogni ingresso in ciascuno di questi CASE.

Interpretare il codice è più semplice che capire la descrizione a parole:

<CODICE>

Sub AvanzamentoDelloStato(StatoDellAutoma As Integer, Ingresso As Integer)

Select Case StatoDellAutoma

Case 1 ' Stato di riposo

Select Case Ingresso

Case 1 ' es. bottone 1 premuto

' transizione allo stato indicato dal grafo, da stato 1 con

' ingresso 1:

StatoDellAutoma = 2

' azione (eventuale) conseguente a questo passaggio di stato

Call AzioneBottone1

' Nota: questa procedura può fare ben di più che accendere una

' lucina od un motorino, come capita con gli automi

' realizzati interamente in Hardware!

Case 2 ' es. bottone 2 premuto

' transizione allo stato indicato dal grafo, da Stato 1 con

' ingresso 2:

StatoDellAutoma = 2 ' rimane nello stesso stato

'in questo caso non fa niente

' [..]

' qui si metterà del codice per ogni ingresso dell'automa

' [..]

Case 3, 5, 7, 21

' caso in cui succedono

Case Else

Debug.Print "Errore: Ingresso non codificato"

End Select

Case 2 ' altro stato

Select Case Ingresso

Case 1

' [..]

' qui si metterà del codice per ogni ingresso dell'automa

' [..]

Case Else

Debug.Print "Errore: Ingresso non codificato"

End Select

' [..]

' si continua così per ogni stato dell'automa non

' [..]

Case Else

Debug.Print "Errore: Stato non codificato"

End Select

End Sub

</CODICE>

Il programma principale potrà essere fatto così:

<CODICE>

Do Until Fine

Call LetturaIngressi(Ingresso) ' lettura del valore dell'ingresso

Call AvanzamentoDelloStato(Stato, Ingresso)

' Stato è un Integer che tiene traccia dello stato dell'automa

' se definito come globale si potrebbe anche evitare di

' passarlo come parametro alla procedura

Loop

</CODICE>

Il programma che viene scritto usando questo approccio è di impostazione molto semplice. Il grafo dell'automa è un potente strumento per la sua documentazione. Un problema di documentazione potrebbe sorgere se l'automa ha molti stati e poche condizioni d'indifferenza. In questo caso la struttura SELECT .. CASE esterna diventa così grande che "in quest'immensità s'affoga il pensier mio" (L'infinito, Leopardi). Dunque si potrebbe perdere il senso di ciò che succede. In questo caso sarà una buona idea ridurre la dimensione della struttura di controllo esterna, facendo chiamate a procedure del tipo:

Select Case StatoDellAutoma

Case 1 ' Stato di riposo

Call MuoviDaStatoUno(Ingresso)

Case 2 ' bottone 2 premuto

Call MuoviDaStatoDue(Ingresso)

' [..]

' e così via ..

Per migliorare ancora la leggibilità, nei linguaggi che lo consentono, come il Pascal, si potrebbe ricorrere ai tipi enumerati, utilizzando quelli invece dei codici numerici assegnati agli stati ed agli ingressi. Se lo si fa il programma si capisce ancora meglio, perché ora gli stati hanno valori che sono nomi significativi e non anonimi valori numerici.

In un programma VB la chiamata a AvanzamentoDelloStato potrebbe essere messa in ogni procedura di evento che determina l'ingresso.

Se, per esempio, simuliamo gli ingressi dal bottone 1 con un CommandButton chiamato Bottone1, la procedura d'evento Bottone1_Click scatterà quando si preme il bottone con il mouse. In questo caso il programma sa già quale è l'ingresso e LetturaIngressi potrebbe anche non esistere.

Esempio:

Sub Bottone1_click

Call AvanzamentoDelloStato (Stato, 1)

End Sub

L'implementazione di automi a stati finiti in programmi "reali" è comune in tutti i casi nei quali è necessario che il programma "capisca" un testo, come succede certamente nel caso dei compilatori, che i miei lettori difficilmente dovranno programmare nella vita reale, o nel caso di applicazioni sofisticate con pagine Web, che sono molto più probabili.